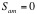Dissertation: Methodology (5 of 8) - Formulae (2)

  and otherwise (Equation 5)

In the case of simulating solar-powered electricity generation, there were two levels of potential obstruction (i.e. clouds and lack of daylight). In the model, the user is able to manipulate both of these by selecting the percentage of cloudiness and by adjusting sunset and sunrise. Initially, the model checks to see if a cloud is covering the solar farm. If so, zero electricity is generated. If not, the model is dependent upon the time of day as described below:

Before noon: , and after noon: .

Before sunrise:   and after sunrise: .

Before sunset: and after sunset: .

Essentially, this generates an equation where the solar farm generates electricity in a sinusoidal pattern – based on the time of day t_day compared to sunrise T_sunrise and the length of daylight L_daylight (as determined by the time difference between sunrise and sunset) – during the day and nothing at night.

Unlike intermittent renewable generation sources, traditional generation sources are operated in a manner designed to meet consumer demand for electricity. This greatly simplifies the equations required to simulate them. However, traditional generation sources can also be run in different modes, which can result in different levels of generation from different types of plants. The two primary modes of plant operation are ‘base load’ and ‘peak load’. As the name implies base load plants form the base of generation needs and run more or less constantly. Whereas, peak load plants are only called into operation during times of peak demand. Since the model is organized based on the fuel type of the generation capacity rather than on individual plants, a third mode of operation was created, which was called ‘mixed load’ and denoted that some plants of the fuel type were operating in base load while others were operating in peak load.

The user interface made use of drop-down field forms. Thus, the actual equations required a significant amount of logical coding in order to match each type of generation with the correct mode of operation. In summary: a generation type in base load constantly operated at its nominal capacity, a generation type in peak load only operated if all other generation options were exhausted, and a generation type operating in mixed load operated only to fill the gap between the base load generation and consumer demand. Also, if multiple types of generation were operating in mixed or peak load, the amount of generation required was distributed evenly among those types but did not exceed the nominal capacity of any particular type.

The user interface offered a choice between having traditional generation account for renewable generation or not. In BL traditional generation needed to take into consideration the electricity generated by renewable sources or else electricity generation did not match demand. In all other scenarios ES rather than traditional generation moderated the renewable generation.

Due to the distinction in GHG emissions, spinning reserve generation was delineated from normal operation. Only generation types operating in mixed load were called into service to operate in spinning reserve. Further, the total generation (i.e. the combination of normal and spinning reserve generation) of each type never exceeded the nominal capacity of that type. It should be noted that this did mean that at least one type of traditional generation needed to be in mixed load for the model to operate properly; however, this is not inconsistent with the real world.

The outputs of the model can be delineated into two groups. The first group of outputs is the diagnostic outputs, which were useful for comparing the model results to the real world and indicating potential errors in the model (see section III.3.d.). The second group of outputs is those highlighted in the results section (e.g. the net GHG emissions and the GHG emissions attributed to ES). The final paragraphs in this section will briefly describe the manner in which the second group of values was calculated.

GHG emissions were calculated in essentially two parts. First, the GHG emissions associated directly with electricity generation was calculated by attributing emissions to each MWh of electricity generation segregated by each type of generation based on the GHG emission rates indicated on the user interface. Also, any spinning reserve generation would have an increased emissions rate. The user interface allowed the proportionate increase in emissions created by fossil-fuel powered plants in spinning reserve to be chosen (non-fossil-fuel powered plants are exempt from this increase because their GHG emissions are associated with construction and decommissioning of the plant rather than plant operation; see section II.2.a. for further explanation). For all scenarios, the value of 0.5 (or a 50% increase in emissions) was applied to plants in spinning reserve mode. Finally, all of these values were summed over all generation types during all intervals to determine the ‘non-ES-related emissions’ and divided by the total electricity generation (measured in MWh) to determine the average rate of emissions for the electricity grid.

Second, the GHG emissions associated with the use of ES were determined by comparing the energy put into storage with the energy withdrawn from storage over the entire week. After accounting for energy losses from the roundtrip cycle efficiency, the model determined how much excess stored energy remained or how much additional energy needed to be produced to make use of the ES. Then, this value was multiplied by the average rate of emissions for the electricity grid as described in the previous paragraph. A positive value of ES-related emissions would indicate that additional emissions (and electricity generation) would be necessary to maintain the use of ES. On the other hand, a negative value would indicate either that electricity generation could have been reduced during the week or depending on the type of ES technology in use that the excess energy could be saved for use during a later time period. Thus, the net GHG emissions are simply the non-ES emissions plus the ES emissions.

Previous Post: Methodology (4 of 8) - Formulae (1)

Next Post: Methodology (6 of 8) - Parameters

Table of Contents - References

Dissertation: Methodology (4 of 8) - Formulae (1)

B.    Formulae

This section outlines the formulae used to calculate the inputs (i.e. electricity demand, renewable generation patterns, traditional generation modes, and spinning reserve) and the model outputs (i.e. net GHG emissions, and GHG emissions attributed to ES). Please note that several of the equations used in this model make use of the random number generator in Microsoft Excel, which produces numbers between -1 and 1. In order to simplify the equations listed below the variable R_x will be used to denote any randomly generated number; however, the use of multiple R_x variables in one equation should be understood to denote multiple random numbers.

Based on the assumptions about electricity demand listed in the section above, the simulated electricity demand D was created using a combination of diurnal D_daily and weekly D_weekly fluctuations as well as fluctuations that represent a frequency shift D_shift similar to that described by Kempton et al (2008). Please see Equation 1 for a detailed view of demand simulation.

  (Equation 1)

Where:

;

with t being the 15-minute time interval;

on weekends or on weekdays;

And with M_day being the maximum demand for the day without including D_shift.

Interestingly, it was discovered that the random number generator created a set of numbers that were not evenly distributed about zero. Whereas in most cases this was not necessarily an issue, in the case of frequency shift, which Kempton et al (2008) explains should contain roughly as much demand for regulation up as regulation down, there was a need for a relatively even distribution. Thus, the bias, which was calculated to be proportionate to 234 for the particular set of random numbers in the model, was subtracted from the random numbers to provide an even distribution in the frequency shift.

By configuring D_curve as it is in the equation above, the daily demand fluctuations reach a minimum at the interval representing 5:00-5:15 a.m. and a maximum at the interval representing 5:00-5:15 p.m. This also means that daily demand fluctuations are about halfway up and halfway down at the interval of 11:00-11:15 a.m. and p.m. respectively. Meanwhile, D_daily is set up to offer a range of variability of up to 10% with regard to the daily maxima and minima on weekdays theoretically centered around 95% of what the inputs for maximum and minimum demands for the week (D_max and D_min respectively) are set to on the model’s user interface. Finally, D_weekly leaves the weekdays unchanged and reduces the demand on weekdays by approximately 10%, which is roughly consistent with the assumptions made in the previous section.

The amount of renewable energy generated on the simulated utility grid is essentially a function of two factors primary: the amount of generating capacity installed and the amount of natural energy (wind or solar rays) available to the system at any particular time. Østergaard (2008) indicates that for renewable energy it is important to consider the effects of the geographic aggregation of all renewable resources on a system. In order to approximate the nuances of a geographically dispersed system, the available renewable generating capacity (Wind_CAP and Solar_CAP) selected on the model’s user interface was divided evenly among 12 different energy ‘farms’ for both wind and solar. Equations 2 and 3 show that the total wind and solar generation (G_w and G_s respectively) are simply the sum of the electricity generated at each of the 12 farms.

  (Equation 2)

(Equation 3)

This segmentation allows for a level of overall wind and solar generation that is more stable than the generation at any particular farm. The individual wind and solar farms (represented as G_wi and G_si respectively) are each respectively governed by Equations 4 and 5 below.

Or

(Equation 4)

Where:

  and  ;

And or .

In the case of simulating wind-powered electricity generation, the user interface of the model allows the user to choose the average availability factor A_f (the proportion of the time that the wind turbines are available for electricity generation; i.e. when the turbines are not broken or under maintenance) and the average capacity factor C_f (the amount of electricity that is typically generated compared to the nominal capacity of the turbines) of the wind turbines connected to the grid.

The choice between G_wA and G_wB simply ensures that the model does not allow a wind farm to generate more than its nominal capacity during any particular interval. While G_wB allows for a random variation of electricity generation centered on the average amount of generation determined by the C_f, A_f, and Wind_CAP settings on the user interface. Meanwhile G_wC means that approximately 5% of the time the wind farm will generate no electricity, which represents intervals with a wind speed below the minimum speed required to turn the blades on the turbines.

Previous Post: Methodology (3 of 8) - Modeling
Next Post: Methodology (5 of 8) - Formulae (2)
Table of Contents - References

Electric Car Review Article

Hello Readers,

There are more dissertation posts coming, but I thought you might be interested in this New York Times review of the new Chevy Volt (and other electric cars).

~Sean

Dissertation: Methodology (3 of 8) - Modeling

3.   Modeling

In addition to the general need to use a simulation tool, Voorspools and D’haeseleer (2000) also highlight the need for “instantaneous” rather than “linear” emission approximations (i.e. not using daily or annual average figures) to accurately determine GHG emissions under varying demand-supply scenarios (Voorspools and D’haeseleer 2000). Despite the need for a sufficiently resolved time-scale, the duration need not be exceptionally long. For example, Verhaegh et al (2010) elected to focus on one-week periods during different seasons (e.g. winter and summer), which suggests that this is a reasonable approach to avoid simulating an entire year’s worth of data.

This study included developing a model in Microsoft Excel, which allowed for the inclusion of a user-friendly interface as well as the ability to make alterations to the model as new types of data were included to increase the accuracy of the model. As a drawback, the Excel-based model could only handle a limited set of calculations before overwhelming the available computing facilities. In order to keep the size of the model within the limitations of the computing facilities available, this study allowed for a time resolution of 15 minute intervals but restricted the simulated time frame to a one-week period, which allowed for sufficient temporal resolution (i.e. as great or greater than that of models described in articles listed in the Reference section) and the inclusion of lower demand periods during the weekend.

In order to develop the model some basic assumptions (see section III.3.a.) were made based on the data gathered regarding ES technologies and electricity generating technologies and electricity consumption patterns in the model region. In some cases these assumptions were used to develop specific formulae that guided the manner in which electricity demand and generation and storage were represented (see section III.3.b.). In other cases these assumptions provided the parameters with which GHG emissions factors and other variables were determined (see section III.3.c.). Naturally, using such assumptions (and the modeling process in general) necessarily limits the accuracy and applicability of the results to real-life purposes (see section III.3.d.).

a.    Assumptions

The first major assumption necessary to build an accurate grid simulation is that the simulated demand for electricity is consistent with actual electricity demand curves. A more accurate demand curve allows for a better understanding of the potential for ES deployment. Officially, PJM recognizes that its ‘on-peak period is all non-holiday weekdays from 7 a.m. until 11 pm and the off-peak is comprised of all other hours’ (PJM 2009). Thus, roughly speaking the demand should be relatively higher between 7 a.m. and 11 p.m. on weekdays than at other times. To simplify matters, this study assumes there all weekdays are non-holidays.

In order to determine the appropriate shape of the diurnal fluctuations and the relative difference between demand on a weekend and on a weekday, historical real-time data was observed on the PJM website (i.e. http://edata2007.pjm.com/eData/index.html). The data observed showed that during the week demand fluctuated between ~70 GW at night and ~120 GW during the day, and the curve appeared roughly sinusoidal reaching about ~90 GW at around roughly 8:30 a.m. and 11:00 p.m. each day. On the weekends, the demand curve showed a roughly similar shape during the night and day; however, the range of the demand was ~62 GW to ~110 GW.

It must be noted that the observation period was not exhaustive (covering only a few days in July). Thus, it is possible that the days observed were not especially ‘normal’; however, this use of real data means the example is not outside the realm of possibility. Furthermore, the observation period does not conflict with any of the other data or reports presented by PJM. As such, the observed data was used as a basis for simulating electric demand (see section III.3.b. for the exact formula used).

The second major assumption made in this study is that over the next two decades the use of bulk ES in the PJM territory is more likely to include a plethora of ES technologies rather than a single type or brand of ES. Therefore, it did not seem prudent to specifically restrict the model to match the exact characteristics of any particular type of ES. Instead, the model was set up to measure the potential for ES use as an output rather than an input. However, to make any useful calculations regarding the impact of ES on GHG emissions it is necessary to make an assumption about the average roundtrip cycle efficiency (i.e. the ratio of usable electricity retrieved divided by the electricity consumed during the storage process) of all the bulk ES in use on the grid.

Rather than speculating about the various proportions of the bulk ES technologies that may be installed over the next two decades, it was simply assumed that for all scenarios the average roundtrip cycle efficiency was 75%. This ratio was chosen because it fell safely within the range of roundtrip cycle efficiencies of all of the bulk ES technologies described in section II.2.a.

Previous Post: Methodology (2 of 8) - Model Region and Scenario Selection
Next Post: Methodology (4 of 8) - Formulae (1)
Table of Contents - References

Small Break and Sustainability Fact & Myth

Hello Readers,

As you may have noticed, I have been on a short break as I attempted to wrap up many loose ends at work before the year ended. As a result, I am only midway through posting my dissertation. I will try to make sure that the rest of the dissertation is posted within the next couple weeks.

In the meantime, I have run across an interesting post about holiday facts and myths related to the holidays. It may be too early to do anything about these suggestions this year, but hopefully you can keep them in mind for next year!

Merry Christmas & Happy Holidays!

Sean Diamond

Dissertation: Methodology (2 of 8) - Model Region and Scenario Selection

2.   Model Region and Scenario Selection

Voorspools and D’haeseleer (2000) stress the need for a simulation tool, stating: “Since it would be impractical to constantly monitor the instantaneous composition of the power system and to calculate (or measure) the corresponding emissions… [f]or studies or scenarios carried out for future or hypothetical developments, monitoring is not even an option and, hence, a simulation tool is essential.” However, a simulation is only really useful to the extent that it is analogous to situations in the real world. In order to maximize the similarities between the model developed in this study and the real world, this study based its characteristics around a real utility grid (i.e. the PJM Interconnection in the USA) and developed scenarios based around plausible alterations to the electricity generation and ES capacity within the established timeline (i.e. prior to 2030).

Initially, this study focused on the PJM region due to its relative familiarity to the author. However, upon even superficial inspection the PJM Interconnection turned out to be perhaps the most appropriate choice. As Boston and Mansoor (2010) explain during an introductory presentation at the PJM-EPRI Energy Storage Summit held in April 2010 the PJM is actively partnering with other companies and organizations to pursue increased deployment of ES within its territory in the immediate future. This ES-friendly sentiment is unequivocally expressed by PJM’s CEO with the need for “Storage, Storage, and More Storage” with regard to the future development plans of PJM (Boston and Mansoor 2010). Furthermore, since PJM covers 168,500-square-miles and roughly 51 million residents in the Northeastern and Midwestern USA (PJM 2010), it is likely that any decisions that PJM makes with regard to future grid development will significantly impact the decisions made by (and subsequently the GHG emissions of) other grid operators across the USA if not the world at-large. Thus, by choosing the PJM territory as a model region the results from this study should be more widely, though less precisely, applicable to the real world beyond the geographic limits of the PJM itself.

This paragraph briefly summarizes some of the characteristics of the PJM territory that were immediately relevant in setting up the model and using PJM as the model region (refer to Appendix C for a full list of PJM statistics considered in this study). In 2009 the annual peak load for the PJM was nearly 145 GW and approximately 729,000 GWh of electricity was generated (Boston and Mansoor 2010). Thus, the PJM has an annual load factor (actual electricity generated divided by the amount of energy that would have been generated if electricity demand was constantly at the peak load; see Söderholm 2001 for a further explanation of load factor) of approximately 0.58. Schainker (2010) states that most of the PJM territory has geography that is suitable for ES (specifically CAES) including a number of depleted gas fields. Finally – and importantly for calculating GHG emissions – ‘marginal’ power plants (i.e. those running at suboptimal generation) produce approximately 60% (with a range of approximately 45-78%) more GHG emissions per unit of electricity generation on average than those running at optimal capacity (PJM 2009).

The four scenarios (plus one baseline scenario) evaluated in this study are based upon possible alterations to the generation capacity utilized within the PJM.

The baseline scenario (BL) generalized somewhat but matched the percentage of generation technologies used during 2009 as closely as possible. Traditional non-intermittent generators met over 95% (most of which was nuclear (~35%), coal (~50%), and natural gas(~10%)) of the electricity demand in the PJM during 2009 (see Appendix C for exact figures). The PJM currently has about 2.8 GW of installed wind capacity and much less than 1 GW of installed solar capacity (Boston and Mansoor 2010). It should also be noted that unlike all of the other scenarios, in BL the model assumed that any gap between the electricity demand and supply was filled by importing additional electricity from neighboring grids. Since information was not collected about the neighboring grids, the assumption was made that all additional electricity would have the same GHG emissions rate as the average of the electricity generated within the territory.

Scenario One (S1) used the same generation percentages as BL; however, S1 used ES capacity rather than importing electricity to meet additional demand. Scenario Two (S2), Scenario Three (S3), and Scenario Four (S4) altered the generation capacities used by the grid. S2 and S3 both have an installed wind capacity of nearly 40 GW, which is similar to the amount of wind capacity that is already committed to be installed in PJM in the near future (Boston and Mansoor 2010). In S2 the increased wind capacity is offset by a proportionate decrease in nuclear, coal, and natural gas capacity. Whereas, in S3 nuclear capacity is actually increased and coal and natural gas capacity are significantly decreased. In S4 both wind and solar capacity are increased significantly beyond the levels simulated in S2 and S3 with nuclear, coal, and natural gas capacity decreased below BL.

In BL and all other scenarios the demand curve is kept the same (see section III.3. for more detail). In S2, S3, and S4 oil capacity (which accounts for about 0.25% of BL capacity) was dropped to zero. In contrast in S2, S3, and S4, traditional hydroelectric capacity (which accounts for about 0.1% of BL capacity) was maintained at a constant level. Please see Table 2 for a comparison of all generation capacities relative to BL.

Table 2: This table compares the quantity of generation capacity in scenarios S1, S2, S3, and S4 to the generation capacity of the same generation type in scenario BL.

Generation Type	S1	S2	S3	S4
Nuclear	x1.00	x0.67	x1.67	x0.29
Coal	x1.00	x0.66	x0.12	x0.25
Natural Gas	x1.00	x0.34	x0.21	x0.43
Oil	x1.00	x0.00	x0.00	x0.00
Hydro	x1.00	x1.00	x1.00	x1.00
Wind	x1.00	x14.29	x14.29	x42.86
Solar	x1.00	x1.00	x1.00	x150.00

Generally speaking, S1 represents the present conditions of the grid if ES were added without any additional changes. S2 roughly represents business-as-usual conditions with the addition of ES during the time period examined in this study. S3 represents a possible ‘nuclear future’, which is favored by some policymakers attempting to reduce GHG emissions, where ES has been included into the mix. S4 represents a possible ES-anchored ‘renewable future’, which follows a more ambitious attempt to reduce GHG emissions than is currently being pursued in the PJM territory. Thus, with the exception of increasing the share of fossil fuel generation capacity (which is already about 60% of overall generation) this study attempts to cover all plausible future development plans within the model region.

It should be noted that even though S1 has a directly analogous baseline scenario (i.e. BL), there is no such equivalent baseline scenario for S2, S3, or S4. This is because if S3 or S4 are to be pursued, many predict that some form ES will be a mandatory addition to the utility grid (e.g. Salgi and Lund 2008, Lund and Salgi 2009, and Barreto et al 2003). Also, as McIntosh (2010) discusses, utility grids with greater percentages of intermittent renewable generation capacity than the model region – such as the California ISO that has a smaller percentage than that represented in S2 – tend to have electric transmission systems that are under significant stress caused by intermittency issues. Further, during the development and debugging of the model, preliminary test trial runs that did not incorporate ES capabilities in situations similar to S2 produced electricity supply curves that did not match demand, which in the real world would not be acceptable to contemporary electricity consumers in developed countries. Thus, it seemed nonsensical (and unreliable) to try to incorporate such situations in the final results of this study. Instead, it should be sufficient to note that once the inclusion of a certain critical percentage of a grid’s generating capacity consists of intermittent renewable generators either ES or some other method of intervention must be made to maintain a stable grid. Otherwise, the traditional electric utility model of ‘on-demand’ electricity supply would need to be abandoned. 

Previous Post:  Methodology (1 of 8) - Data Collection

Next Post: Methodology (3 of 8) - Modeling

Table of Contents - References

Dissertation: Methodology (1 of 8) - Data Collection

 III.    Methodology

1.   Data Collection

From the outset of this study, which sought to analyze and compare a wide variety of technologies at various stages of research, development, deployment, and use, it was clear that ‘data collection’ would be necessarily complicated. Initially, the expectation was that sufficient data could be collected directly from owners, operators, and manufacturers of ES technologies; however, it soon became apparent that additional supplementary data sources would be required to compile a comprehensive set of parameters for modeling purposes. Thus, a manifold process of data collection was put into action. This process included: (a) identifying and contacting owners, operators, and manufacturers of ES technologies as well as electric utility operators in the model region (i.e. the PJM Interconnection territory in the USA), (b) developing and distributing a suitable survey, and (c) identifying and interpreting supplementary data sources.

a.    Direct Sources

Since the majority of data required to develop modeling parameters is based on technical data related to the performance of ES technologies (many of which are still in the developmental or even research phases), it was expected that it would be difficult to collect first-hand data. Furthermore, due to the nature of grid operations, the time scales needed for analysis, and the limited timeline on which this study needed to be performed, it was deemed necessary to rely upon second-hand information regarding the technical specifications of ES technologies and the electricity grid rather than direct measurements.

Thus, to most directly access the necessary data, it was decided that surveying those who used and manufactured the equipment in question was the most prudent approach. In order to identify appropriate survey recipients, a contact list was compiled by: (1) searching for relevant terms on the Google internet search engine, (2) noting companies that were clearly identified within academic journal articles (e.g. those listed in the Reference section), (3) identifying key individuals who presented at the 2010 PJM-EPRI Energy Storage Summit, and (4) noting the utility companies and regulators listed on the Pennsylvania Public Utility Commission Website (i.e. http://www.puc.state.pa.us/electric/electric_companies.aspx).

b.   Survey Development, Distribution, & Responses

The survey (see Appendix A) was developed with energy storage professionals and utility operators in mind. As such, it includes a brief introduction and some key instructions to explain the purpose of the survey, describes how to complete and submit the survey, and encourages survey recipients to participate. As a limited incentive, all survey participants were offered a free copy of the final version of this dissertation. However, since the intended participants were those who were already knowledgeable of ES and utility systems, there was no explicit technical information provided to the participants within the survey.

The survey distribution process included multiple stages. The first stage (prior to contacting survey participants) included gathering contact information (see section III.1.a. above) and posting information about the dissertation study on a website (i.e. http://seandiamondsustainability.blogspot.com/). The second stage involved making initial contact with potential participants, which was delivered through a variety of media depending on what contact information was available. The majority of participants were contacted prior to the release of the survey using a letter sent via the postal service. The remainder of the participants was either contacted via email or telephone. The third stage involved distributing the actual survey via email and posting it on the website. After the third stage, follow up emails or phone calls were made to participants to encourage them to participate and answer questions or concerns the participants might have.

On a separate note, it should be addressed that though respondents were not given any direct incentive to provide a particular type of answer (i.e. “better” figures) and they were ensured that there responses would not directly identify them, the potential for respondents to give a best-case-scenario response remained a possibility. This was especially the case for ES manufacturers who could stand to benefit financially by making their product seem marginally more beneficial than a competing technology or product. Further, even if there was no intent to provide augmented responses, it should be understood that many of the technologies in question have not necessarily been exhaustively field tested through massive commercial deployment. Unfortunately, due to the nature of this study, there was no a priori way to ensure or measure the reliability of the responses provided. Thus, all survey responses have been taken as truthful and reasonably accurate.

Responses to the proactive, multi-stage survey approach varied. The majority of participants who were contacted did not respond at all. However, some (approximately 20%) responded positively to the initial contact and follow up attempts. Unfortunately, the final response rate (i.e. those who completed and submitted a survey response by or soon after the submission deadline) was abysmally low (approximately 6%) and did not yield sufficient data upon which to establish modeling parameters. Since the survey responses were ultimately not useful for the end results of this study, they were not included in attempts develop model parameters.

c.    Supplementary Sources

The initial expectation of using supplemental sources of information to fill in any gaps left by the survey responses ended up being an underestimation of their value. Ultimately, secondary sources (i.e. academic journal articles) and data compiled by the PJM regulatory authority for other purposes (e.g. public relations reports) were indispensible sources of data in this study. Furthermore, despite their label as supplementary sources, the entirety of the modeling parameters were established based on the information obtained from these sources. For a full list of the data compiled from supplementary sources see Appendix B (information regarding ES technologies) and Appendix C (information regarding the model region).

Previous Post: Background (3 of 3) - Plug-in Electric Vehicles

Next Post: Methodology (2 of 8) - Model Region and Scenario Selection

Table of Contents - References

Dissertation: Background (3 of 3) - Plug-in Electric Vehicles

c.    Plug-in Electric Vehicles

Kempton (2010) discusses the potential for plug-in EVs using ‘Vehicle-to-Grid’ (V2G) controls to alleviate the need for other forms of technology to maintain ancillary grid services (particularly spinning reserve and frequency regulation). Most cars in the USA are only used for 1 hour per day and have oversized batteries for the occasional long trip. V2G controls allow for a two-way flow of power, which utilizes the spare capacity of the vehicle’s battery to respond to demand for regulation services (Kempton 2010). Kempton et al (2008) show that this technology can successfully be employed to simultaneously meet the needs of the average driver as well as the needs of the grid throughout the course of a day. This has much to do with the nature of frequency regulation, which typically requires both regulation-up and -down several times throughout the course of an hour. Therefore, the vehicle’s battery need not be completely drained or filled to provide regulation services (Kempton et al 2008).

Furthermore, the incorporation of V2G means that vehicle owners will be compensated by utility companies for their services (Kempton et al 2008), which may provide additional incentives for car owners interested in switching from combustion-engine vehicles to EVs. In other words, the use of V2G may facilitate the reduction of GHG emissions more than simple ES or non-V2G EVs by reducing the number of traditional cars and by allowing for the benefits illustrated elsewhere in this study. This solution may be particularly appealing in the USA where the transportation system is dominated by the use of personal cars. In fact, Kempton (2010) optimistically estimates that within the next ten years (i.e. during the first half of the time period this study is considering) half of the fleet in the PJM territory could be plug-in EVs, which could provide 15 GW (30 GWh) of ES (or approximately 1 MW of ancillary ES for every 100 plug-in EVs). Finally, an additional benefit of using V2G rather than other alternative forms of ancillary ES is that utilities can avoid the bulk of additional costs because they only need to pay for the smart-grid controls while the owners of the vehicles pay for the battery systems.

Whether utility companies elect to rely upon plug-in EVs, the ancillary ES technologies highlighted in section II.2.c., or some combination of the two, it is clear that within the next two decades ancillary grid needs could be met without relying solely upon traditional fossil-fuel generator capacity. Thus, this study shall consider the need for a minimum amount of such capacity to no longer be the strict limiting factor suggested by previous studies (e.g. Østergaard 2006 & 2008).

Previous Post: Background (2 of 3) - Energy Storage Technologies

Next Post: Methodology (1 of 8) - Data Collection

Table of Contents - References